Relative Motion

A person swims in a river aiming to reach exactly opposite point on the bank of a river. His speed of swimming is $0.5\hspace{0.17em}\mathrm{m}\mathrm{\hspace{0.17em}}{\mathrm{s}}^{-1}$ at an angle $120°$ with the direction of flow of water. The speed of water in stream is:

A boat is sent across a river with a velocity of $8 \mathrm{km }{\mathrm{hr}}^{-1}$. If the resultant velocity of the boat is $10 \mathrm{km} {\mathrm{hr}}^{-1}$, then the velocity of the river is

On a frictionless horizontal surface, assumed to be the $x – y$ plane, a small trolley $A$ is moving along a straight line parallel to the $y$– axis (see figure) with a constant velocity of  $\left(\sqrt{3}-1\right)m{s}^{-1}$ . At a particular instant, when the line $OA$ makes an angle of  $45°$  with the $x$-axis, a ball is thrown along the surface from the origin $O$. Its velocity makes an angle $\theta$ with the $x$-axis and it hits the trolley.​
The motion of the ball is observed from the frame of the trolley and the velocity vector of the ball makes an angle $$$\varphi$$$with the x-axis in this frame.


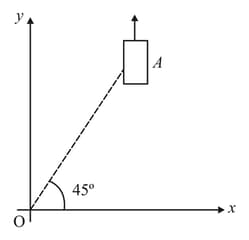
Find the speed of the ball with respect to the surface if  $\varphi =\frac{4\theta }{3}.$

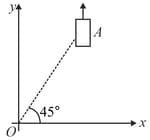
On a frictionless horizontal surface, assumed to be the x-y plane, a small trolley A is moving along a straight line parallel to the y-axis (see figure) with a constant velocity of $\left(\sqrt{3}-1\right)m{s}^{-1}$. At a particular instant, when the line OA makes an angle of $45°$ with the x-axis, a ball is thrown along the surface from the origin O. Its velocity makes an angle $\varphi$ with the x-axis and it hits the trolley. The motion of the ball is observed from the frame of trolley. Calculate the angle $\theta$ made by the velocity vector of the ball with the x-axis in this frame.

A ball is thrown from a point with a speed $v_0$  at an angle of projection $\theta$ . from the same point and at the same instant, a person starts running with a constant speed  $\frac{v_0}{2}$ to catch the ball. will the person be able to catch the ball? If yes, what should be the angle of projection?

A river is flowing from west to east at a speed of $5 \mathrm{m}$ per minute. A man on the south bank of the river, capable of swimming at $10 \mathrm{m}$ per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction

Four persons $K$, $L$, $M$, $N$ are initially at the four corners of a square of side $d$. Each person now moves with a uniform speed  $v$ in such a way that $K$ always moves directly towards $L$, L directly towards $M$, $M$ directly towards $N$, and $N$ directly towards $K$. The four persons will meet at a time

A river has a steady speed of $v$. A man swims upstream at a distance of $d$ and swims back to the starting point in total time $t$. The man can swim at a speed of $2v$ in still water. If the time taken by the man in still water is $t_0$ to complete the same length of swim, then $\frac{t}{t_0}$ is

An aeroplane travels at the speed of $400 \mathrm{km} {\mathrm{h}}^{-1}$. It ejects its products of combustion at the speed of $1200 \mathrm{km} {\mathrm{h}}^{-1}$ with respect to an observer on the ground. The speed of ejected product of combustion relative to the aeroplane is

A river flows with a speed more than the maximum speed with which a person can swim in still water. He intends to cross the river by the shortest possible path, (i.e., he wants to reach the point on the opposite bank which directly opposite to the starting point). Which of the following is correct?

Raindrops are falling vertically with a velocity $10 \mathrm{m} {\mathrm{s}}^{-1}$. To a cyclist moving on a straight road, the raindrops appear to be coming with a velocity of $20 \mathrm{m} {\mathrm{s}}^{-1}$. The velocity of the cyclist is

The speed of a motorboat in still water $20 \mathrm{km} {\mathrm{hr}}^{-1}$ And river flow is $5 \mathrm{km} {\mathrm{hr}}^{-1}$. A float is dropped from the boat when it starts moving upstream. After moving $1.5 \mathrm{km}$ The boat returns. The boat will catch the float (from initial instant) after;

 Two men, $P$and $Q$ are standing at corners $A$ and $B$ of a square $ABCD$of side $8 \mathrm{m}$. They start moving along the track with constant speed $2 \mathrm{m} {\mathrm{s}}^{-1}$ and $10 \mathrm{m} {\mathrm{s}}^{-1}$, respectively. Find the time when they will meet for the first time.

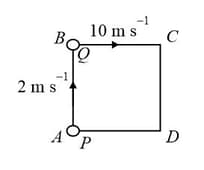
A man crosses a river perpendicular to the river flow in time $t$ and travels an equal distance down the stream in time $T$. The ratio of man's speed in still water to the speed of river water will be :

Consider a collection of a large number of particles each moving with speed $v$. The direction of velocity is randomly distributed in the collection. Find the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection.

A car A is moving with speed $40 \mathrm{km} {\mathrm{h}}^{-1}$ along a straight line $30°$ north of east and another car B is moving with same speed along a straight line $30°$ south of east. The relative velocity of car A as observed from the car B is

For four particles $A,B,C$ and $D$, the velocities of one with respect to others are given as, $\overrightarrow{V_{DC}}$ is $20 \mathrm{m} {\mathrm{s}}^{-1}$ towards north, $\overrightarrow{V_{BC}}$ is $20 \mathrm{m} {\mathrm{s}}^{-1}$ towards east and $\overrightarrow{V_{BA}}$ is $20 \mathrm{m} {\mathrm{s}}^{-1}$ towards south. Then $\overrightarrow{V_{DA}}$ is

A boat is sent across a river with a velocity of $8\mathrm{km }{\mathrm{hr}}^{-1}.$ If the resultant velocity of the boat is $10\mathrm{km}{\mathrm{hr}}^{-1},$ then the velocity of the river is

Assertion : Path of a projectile, seen from another projectile is straight line.

Reason : If relative acceleration is zero then relative velocity will be constant.

Assertion : Three projectiles are moving in different paths in the air. Vertical component of relative velocity between any of the pair does not change with time as long as they are in air. Neglect the effect of air friction.

Reason : Relative acceleration between any of the pair of projectiles is zero.